
Décollage des aéronefs
Iliona & Marine
Étude de la portance Rz en fonction de la vitesse V
La portance est une force qui s'exprime de la manière suivante:
Rz = ½ ρ S Cz V²
avec ρ= 1,267 kg.m^-3
S= 13,6 m²
Cz= 0,10
D'après nos calculs précédents, on sait que:
Rz (V) = ½ * 1,267 * 13,6 * 0,10 * V²
= 0,1 V²
On remarque que Rz (V) = a*V² avec a = 0,1.
a = 0,1 est strictement supérieur à 0,
donc la fonction Rz a le même sens de variation que la fonction carré sur [0; + ∞ [
donc la fonction Rz est croissante sur [0; + ∞ [.
Cela signifie que plus la vitesse augmente, plus la portance augmente.
Étude du coefficient de portance Cz en fonction de l'angle d'incidence α :
On représente graphiquement Cz, coefficient de portance en fonction de α, l'angle d'incidence.
Le graphique Cz (coefficient de portance) est construit à partir des valeurs de la force Rz (portance) en fonction de l’angle d’incidence α de l’aile par rapport au vent relatif.
Ces valeurs ont été mesurées expérimentalement.

On construit le graphique

Le nuage de points ainsi obtenu peut laisser penser que la courbe représentative de la fonction Cz ressemble à une parabole.
On en déduit que Cz(α) = aα²+bα+c.
A l'aide de la calculatrice, on va déterminer les valeurs des coefficients a, b et c.
On pose x = α, cela devient: Cz(x) = ax²+bx+c.
Afin d'obtenir l'expression de la fonction Cz; on saisit le tableau numéro 1 dans la calculatrice, où la liste 1 correspond aux valeurs de α et la liste 2 correspond aux valeurs
de Cz.
On obtient: a= -0,0015 b= 0,0842 c= 0,1199
On peut ainsi écrire que Cz (x) = -0,0015x²+0,0842x + 0,1199.
Déterminons les coordonnées du sommet de la parabole Cz en fonction de α
Les coordonnées du sommet de la parabole d'une fonction du second degré sont ( α; β).
On sait que α= et β= f(α).
On note α = l'abscisse du sommet = = = 28,1
β = l'ordonnée du sommet = f(28,1) = 1,30
Remarque: On observe cependant que l'approximation de la parabole n'est pas celle que l'on attend car elle ne passe pas par le sommet modélisé par le nuage de points.
La courbe de tendance semble avoir un sommet bien plus éloigné que notre fonction.
Nous en déduisons donc que nos valeurs sont trop étendues. Nos calculs ne correspondent donc pas à notre graphique.

Pour obtenir une courbe de tendance plus juste, on choisit de rétrécir notre tableau: on ne conserve que les valeurs de 10 à 18.
Nouveau graphique obtenu

Calculs des coordonnées du sommet de la parabole Cz en fonction de α :
On note α = l'abscisse du sommet = = = 16,09
β = l'ordonnée du sommet = f(16,09)= 1,096
a = - 0,008 est négatif
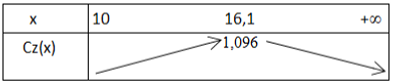
donc la fonction Cz est croissante sur l'intervalle [10; 16,1]
et est décroissante sur l'intervalle [16,1; +∞ [.
De plus, la fonction Cz admet un maximum, égal à 1,096, atteint en α = 16,1.
Tableau de variation de la fonction Cz:
Quelles interprétations peut-on faire?
1) La partie croissante de la courbe traduit le fait que plus l’angle d’incidence est élevé, plus la portance est forte.
2) La valeur du sommet atteint en α est la valeur donnant la portance maximale.
3) La partie décroissante de la courbe traduit le décrochage et donc la perte de portance.
Ainsi au-delà de 16 degrés, les filets d'airs se décrochent de la pales ou de l'aile: c'est le décrochage.